인덱스란
- 데이터베이스 테이블의 검색 속도를 향상시키기 위한 자료구조로, 사전의 목차와 유사하다.
- 저장되는 컬럼의 값을 사용하여 항상 정렬된 상태를 유지합니다.
- 이러한 특징으로 인덱스는 쓰기 작업인 Insert, Update, Delete 연산 성능이 희생된다는 장점이 있습니다.
- 하지만 데이터베이스 작업은 읽기 작업이 80% 정도 일어나므로, 인덱스를 사용하는 것이 더 큰 장점이 있습니다.
InnoDB 스토리지 엔진에서는 Secondary Index(Primary Index를 제외한 모든 인덱스)의 리프 노드에는 레코드의 PK가 저장됩니다. 따라서 Secondary Index 검색에서는 레코드를 읽기 위해 PK를 가지고 있는 B-Tree를 다시 한번 검색해야 합니다. (1 + 1)
B Tree
자녀 노드의 최대 개수를 늘리기 위해서 부모 노드에 Key를 하나 이상 저장하는 자료구조.
이진 탐색 트리를 일반화한 트리라고도 합니다.
- Root Node: 최상위에 있는 노드
- Branch Node: 루트 노드와 리프 노드 중간에 있는 노드
- Leaf Node: 가장 하위에 있는 노드
- 리프 노드에는 실제 데이터 레코드를 찾아가기 위한 주소값을 가지고 있습니다.
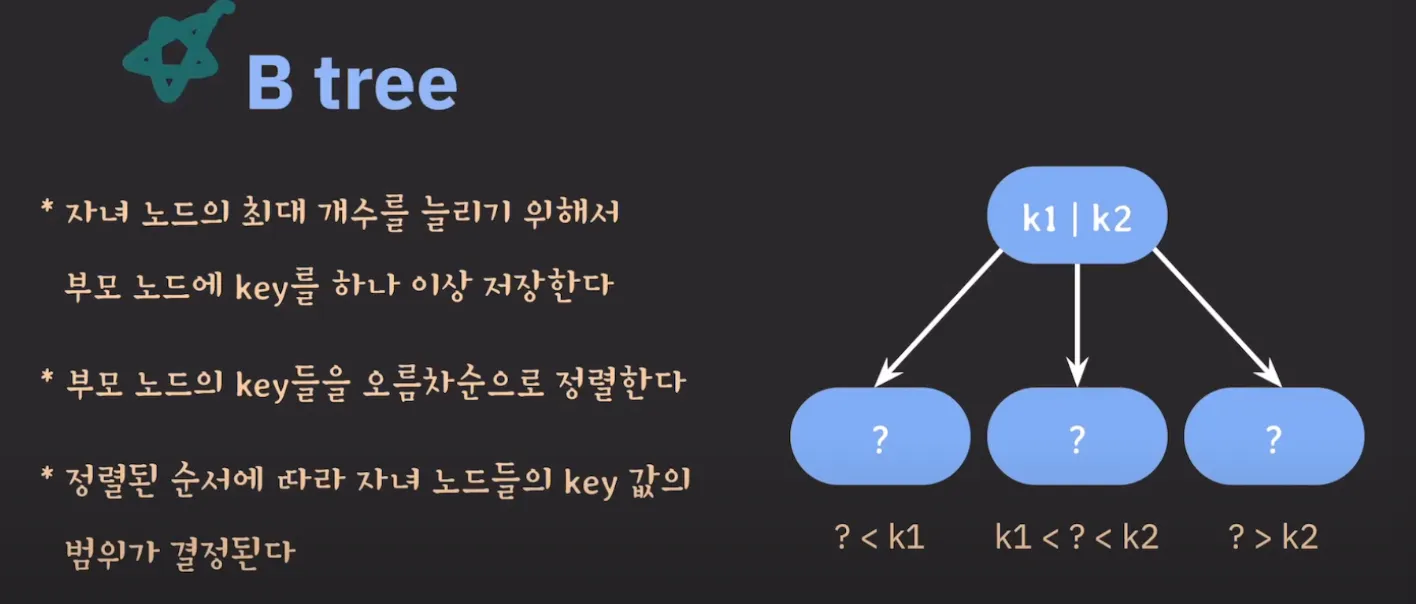
- 부모 노드의 Key들을 오름차순으로 정렬합니다.
- 정렬된 순서에 따라 자녀 노드들의 key 값의 범위가 결정됩니다.
- ? < k1 / k1 < ? < k2 / ? > k2
B Tree 파라미터
- M : 각 노드의 최대 자녀 노드 수
- M이 3인 경우, 3차 B-Tree라고 부름
- M-1 : 각 노드의 최대 Key 수
- M을 정하면 자동으로 설정됨. M이 3인경우 각 노드의 Key는 최대 2개까지 가질 수 있음
- ⎡M/2⎤ : 각 노드의 최소 자녀 개수
- 3차 B-Tree에서는 최소 2개의 자녀 개수를 가집니다. (root node, leaf node 제외)
- ⎡M/2⎤ -1 : 각 노드의 최소 Key 수
- 3차 B-Tree에서는 최소 2개의 Key를 가집니다. (root node 제외)
잘못된 B-Tree 구조 보기

- Key가 2개인데, 자녀 노드의 개수가 2개이므로 잘못된 구조이다.
- Key가 3개이면 자녀 노드의 개수는 3개여야 함.
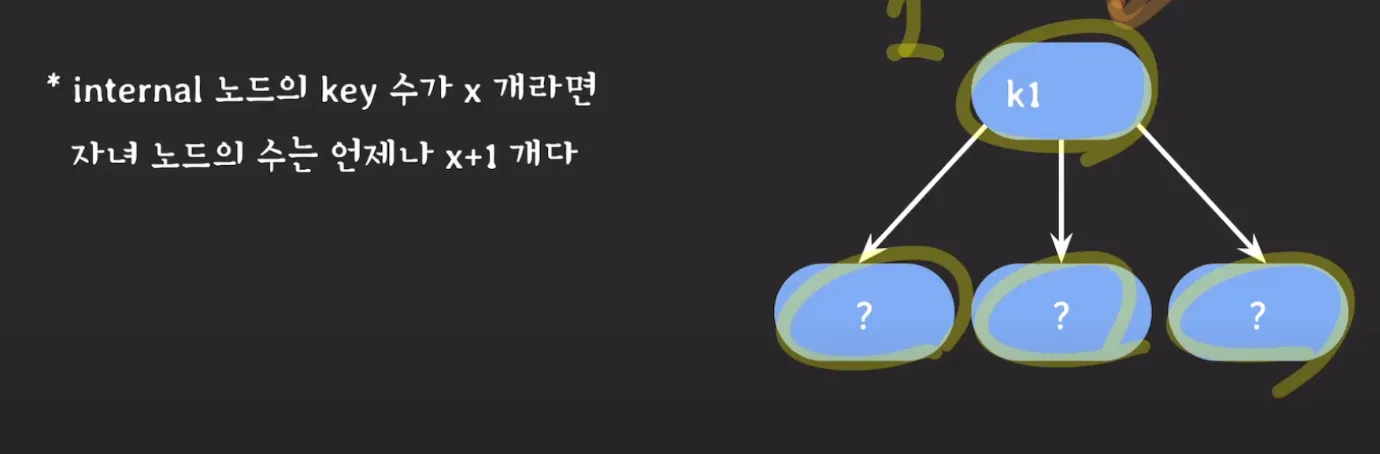
- Key가 1개인데, 자녀 노드의 개수가 3개이므로 잘못된 구조이다.
B-Tree
노드가 최소 하나의 Key는 가지기 때문에, N차 B-Tree인지와 상관없이 internal 노드는 최소 2개의 자녀 노드를 가집니다.
B Tree 데이터 삽입
- 추가는 항상 leaf 노드에 한다. (오름차순 순으로 추가한다.)
- 노드가 넘치면 가운데 Key를 기준으로 좌우 Key들은 분할하고, 가운데 Key는 승진한다.
- 노드가 넘친다 == 노드가 가질 수 있는 자녀의 개수 (M)
예시 1
1/2/15 key가 저장된 B Tree
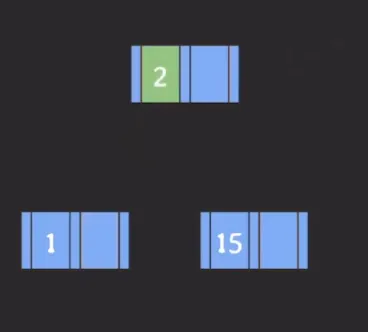
2를 기준으로 왼쪽은 작은 값, 오른쪽은 큰 값이 저장된다.
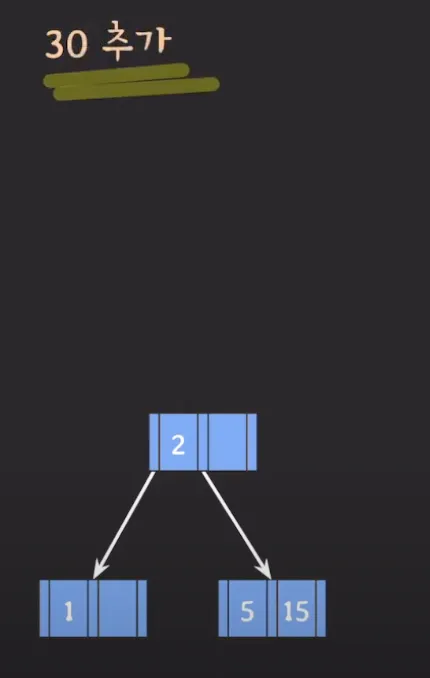
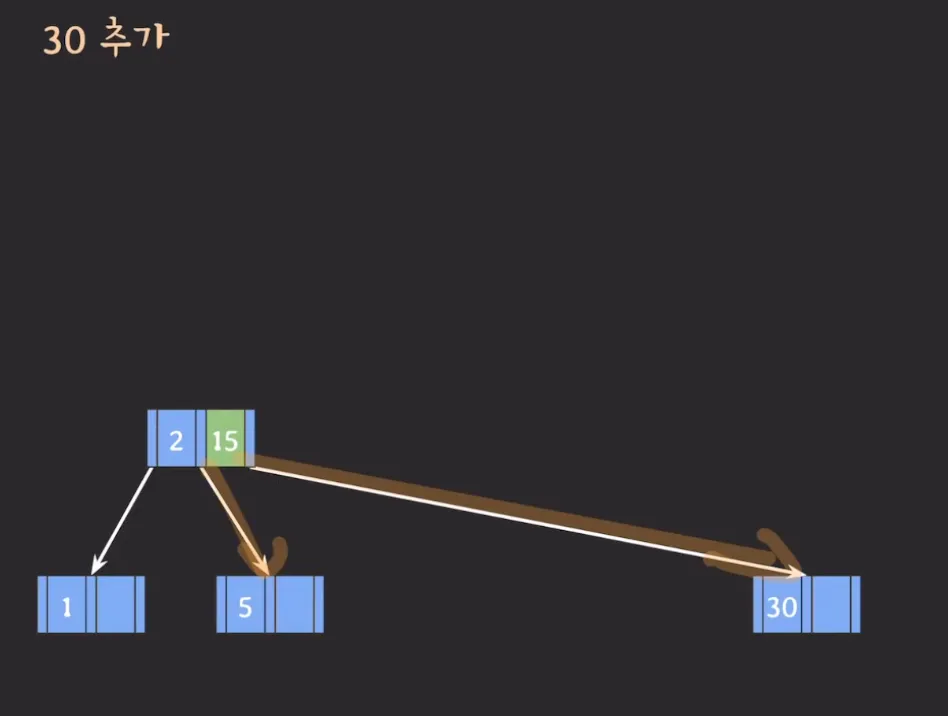
- 위 상태에서 30이 추가되면 오른쪽 아래에 있는 노드에 추가되어 5, 15, 30 값을 가지게 됩니다.
- 3차 B Tree이므로 각 노드는 최대 2개의 Key를 가질 수 있으므로 변동이 필요합니다.
- 가운데 있는 15가 부모 노드로 승진합니다.
- 30은 15보다 크므로 3번째 자녀 노드에 위치시킵니다.
예시 2
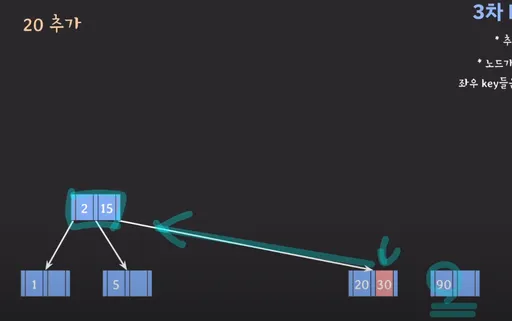
현재 상황은 3번째 자녀 노드에 30, 90이 저장된 상태에서 20이 추가된 상황입니다.
- 20은 15보다 크므로 3번째 자녀 노드에 들어갑니다.
- 가운데에 있는 30은 부모 노드로 승진하고 90은 분리됩니다.
- 30이 부모 노드로 승진하면 부모 노드는 3개의 Key를 가지게 되어 변동이 필요합니다.
- 가운데에 있는 15 값을 부모 노드로 승진시킵니다.
- 승진 되면서 2와 30 값을 분리합니다.
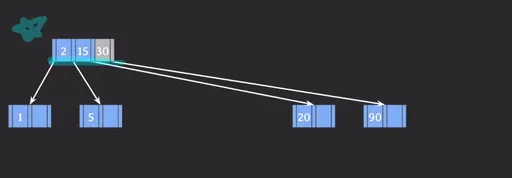
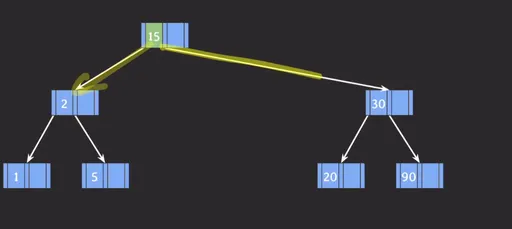
예시 마지막 결과
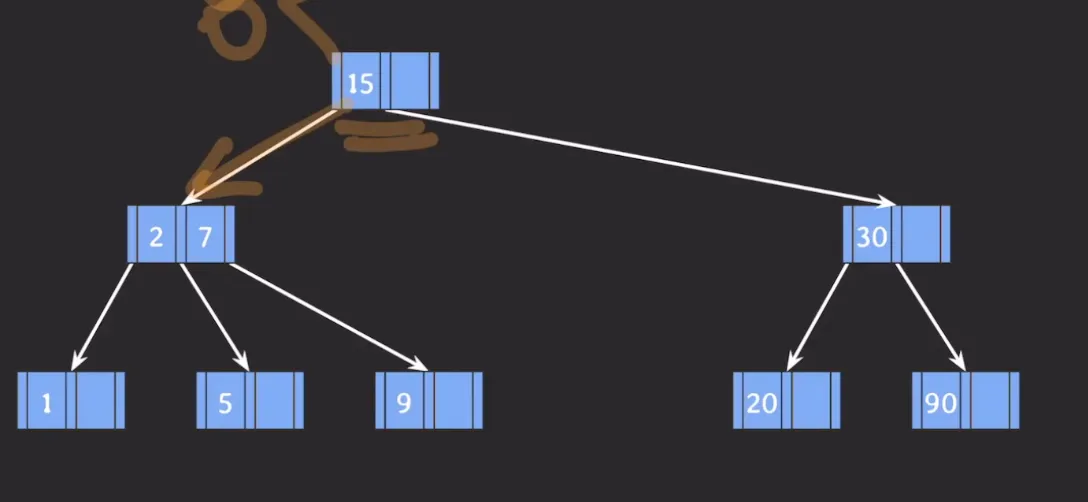
B Tree 데이터 삭제
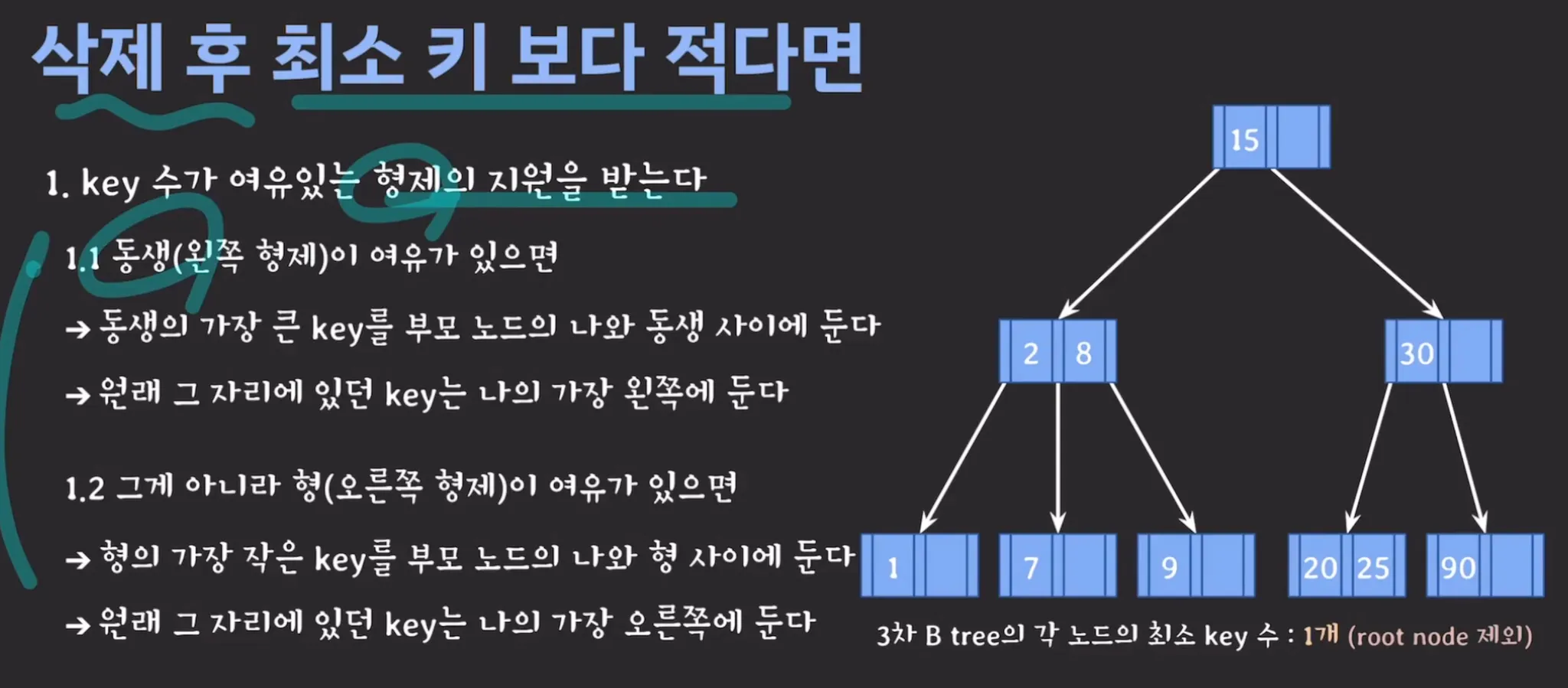
🔥 B Tree 계열을 Index로 사용하는 이유
먼저, 데이터베이스가 어디에 저장되고, 어떻게 조회하고 있는지 파악하기
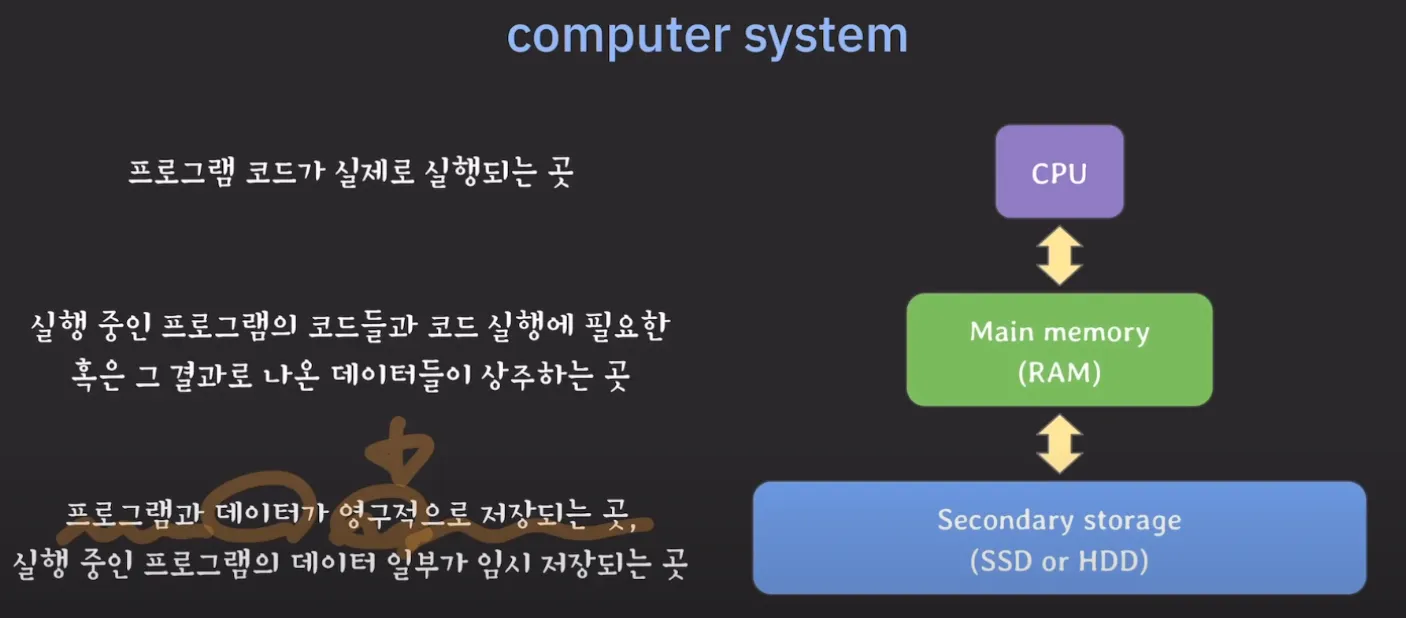
Secondary Storage
- 데이터를 처리하는 속도가 가장 느리다.
- 데이터베이스는 보통 Secondary Storage에 해당함
- 데이터를 저장하는 용량이 가장 크다.
- Block 단위로 데이터를 읽고 쓴다.
- file system이 데이터를 읽고 쓰는 논리적인 단위
- block의 크기는 2의 승수로 표현된다.
- 불필요한 데이터까지 읽어올 가능성이 있다. (불필요한 데이터가 발생할 수 있음)
DB 관점 Secondary Storage
- DB에서 데이터를 조회할 때 최대한 적게 접근하는 것이 성능면에서 좋다.
- I/O 속도가 느리기 때문에
- block 단위로 읽고 쓰기 때문에, 연관된 데이터를 모아서 저장하면 더 효율적으로 읽고 쓸 수 있다.
- 추가로 조회된 데이터가 연관이 있는 경우, 추가 조회 없이 데이터를 조회할 수 있다.
AVL Tree vs B Tree
AVL Tree도 B Tree와 마찬가지로 모든 연산에 대해 O(log n)의 시간 복잡도를 가지고 있는데, B Tree를 인덱스 자료구조로 사용하는 이유
1. AVL Tree
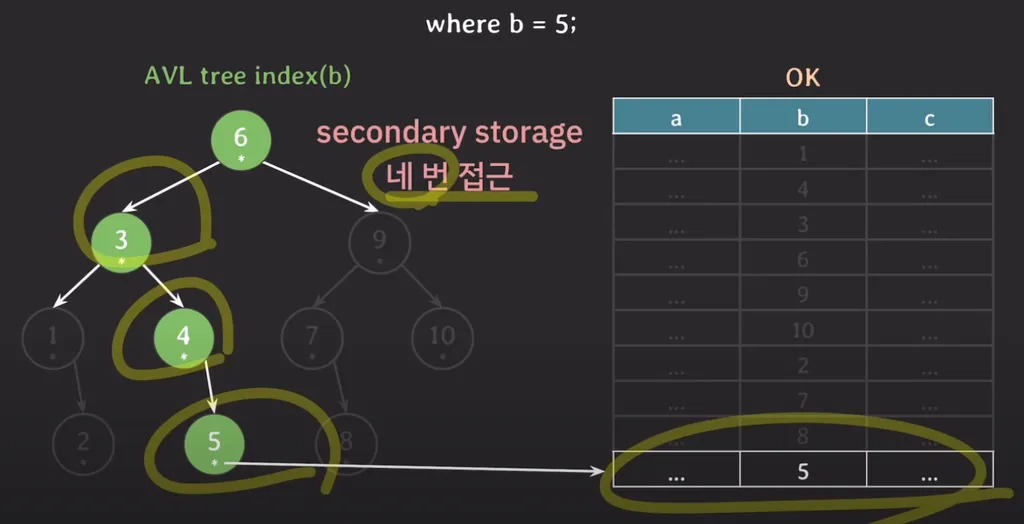
Root Node만 메모리에 올라가 있다고 하면
where b = 5를 탐색할 때
- 3번 노드 (1번 조회)
- 4번 노드 (1번 조회)
- 5번 노드 (1번 조회)
- 5번 노드의 포인터 값 조회 (1번 조회)
- 총 4번의 조회가 발생합니다.
2. B-Tree
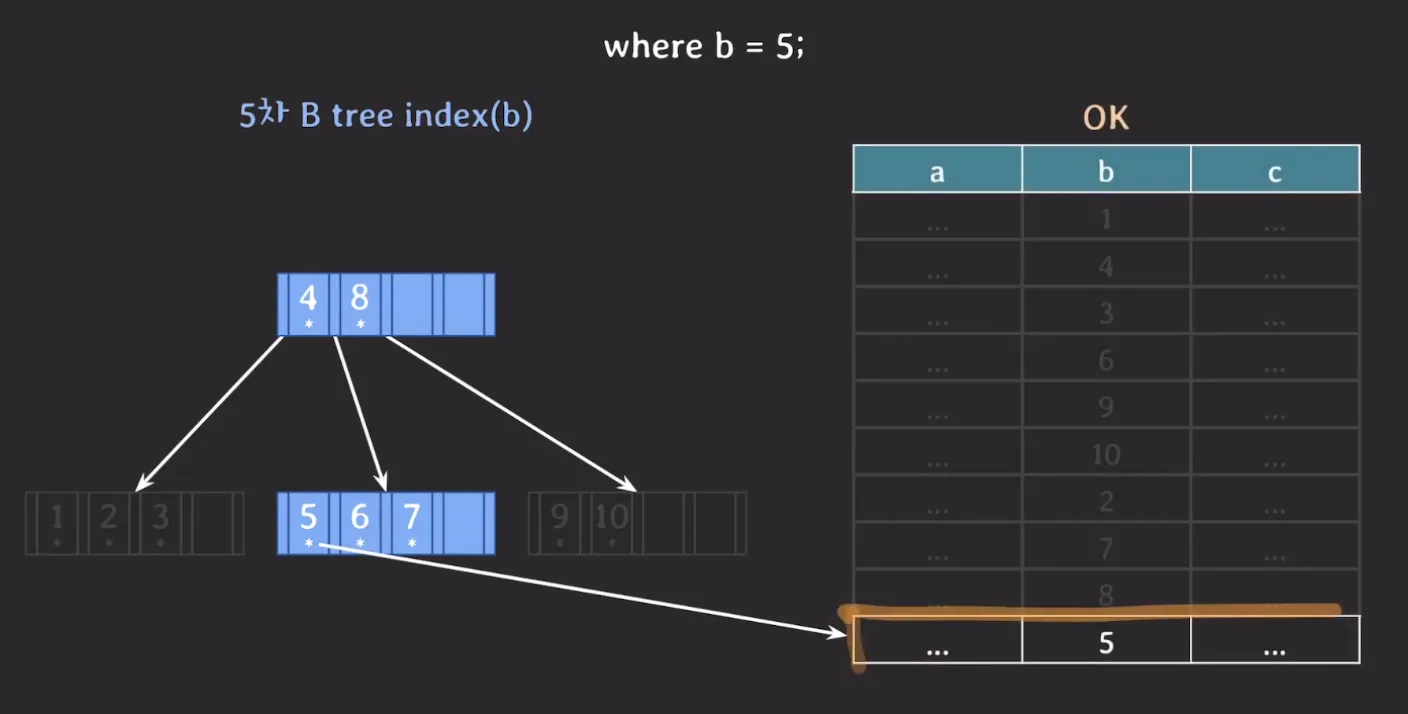
Root Node만 메모리에 올라가 있다고 하면
where b = 5를 탐색할 때
- 가운데 리프 노드 (1번 조회)
- 가운데 리프 노드 5번 Key에 포인터 값 조회 (1번 조회)
- 총 2번의 조회 발생합니다.
AVL Tree vs B Tree 결론
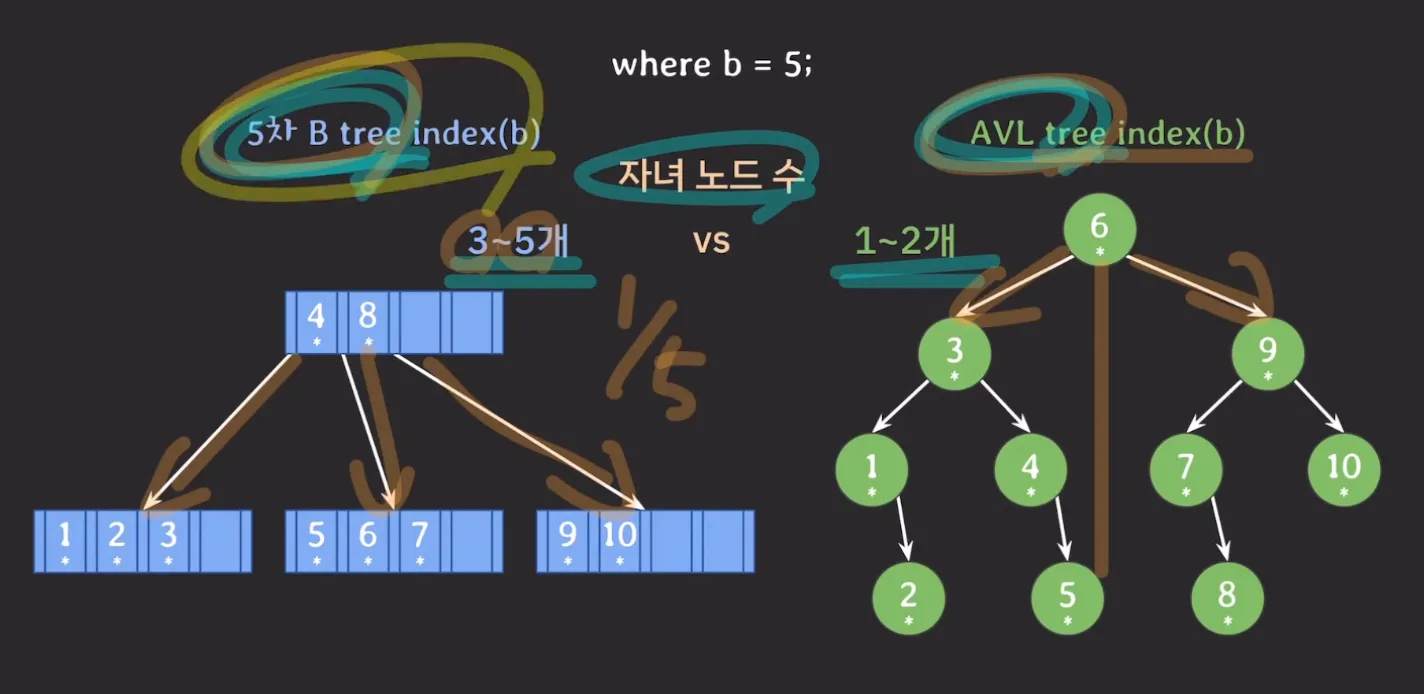
B-Tree는 AVL 트리와 달리, 자녀 노드의 개수를 설정할 수 있어, Secondary Storage와의 조회 요청을 단축시킬 수 있습니다.
데이터를 찾을 때 탐색 범위를 빠르게 좁힐 수 있어, Index 자료구조로 사용된다.
추가 예시) 101차 B-Tree
M = 101 / 하나의 노드는 101개의 자녀 노드를 가질 수 있으며, 100개의 key를 가질 수 있음
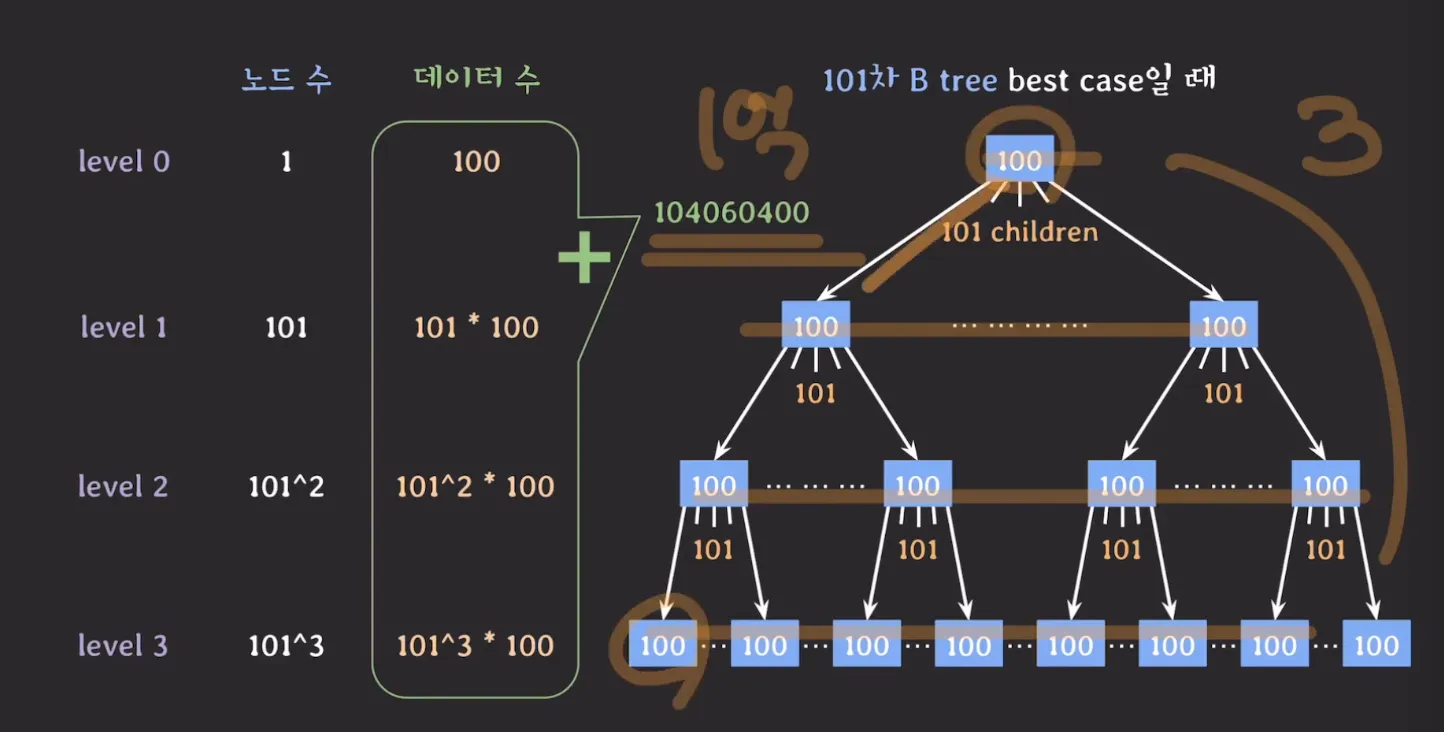
- 높이 3으로 약 1억개의 데이터를 저장할 수 있음
101차 B-Tree Worst Case
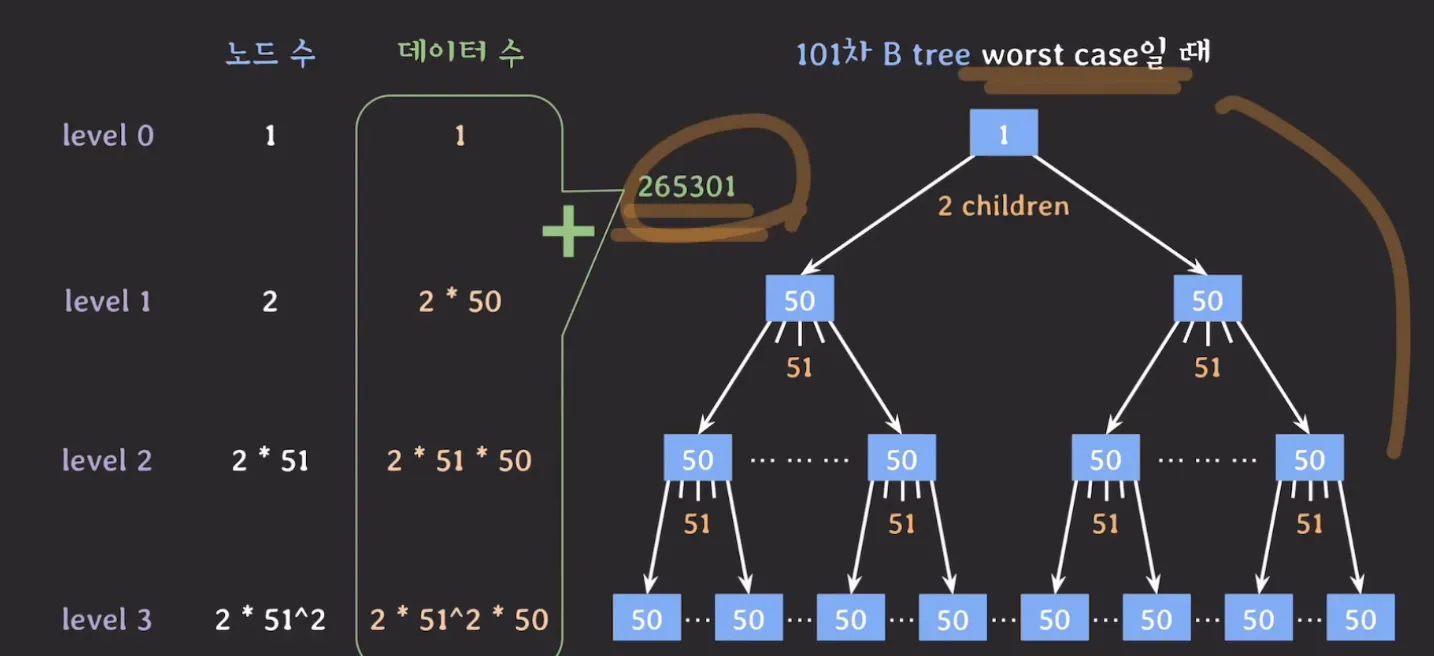
- 4개의 레벨, 높이 3만으로도 수 백만, 수 천만 개의 데이터를 저장할 수 있다.
B Tree 정리
- 자녀 노드의 최대 개수를 늘리기 위해서 부모 노드에 Key를 하나 이상 저장하는 자료구조이다.
- B-Tree는 AVL 트리와 달리, 자녀 노드의 개수를 설정할 수 있어, Secondary Storage와의 조회 요청을 단축시킬 수 있다.
- 노드가 최소 하나의 Key는 가지기 때문에, N차 B-Tree인지와 상관없이 internal 노드는 최소 2개의 자녀 노드를 가진다.
- 101차 B Tree 구조를 통해 26,5301 < avg size < 1,0406,0400 개의 데이터를 4개의 level과 3번의 move로 처리할 수 있다.
B+Tree
B Tree와 차별화된 특징으로는
- B+Tree의 리프 노드는 서로 연결 리스트로 연결되어 있습니다. 형제 노드끼리 옮겨가며 조회가 가능합니다.
- internal 노드에는 Key만 저장되며, 이 Key를 사용해서 자식 노드의 저장공간 상 위치를 판단합니다.
- 데이터를 찾기 위한 포인터도 리프 노드에만 있습니다.
- internal 노드의 데이터 크기를 줄여 메모리 사용이 효율적입니다.
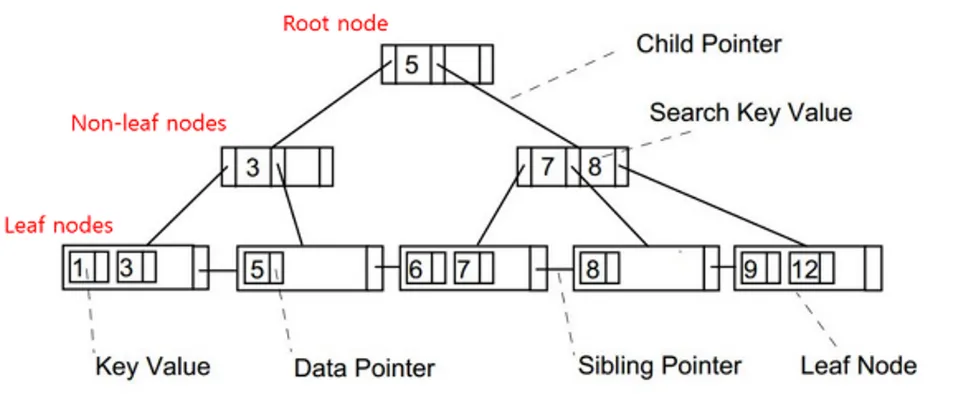
- Root node : 최상단 노드, 검색 경로의 출발점
- Branch node : Leaf node까지 가기 위해 다음 경로 노드의 key 값(데이터를 위한 인덱스)을 가지고 있는 노드
- Leaf node : 인덱스(key)와 함께 실제 검색할 데이터(value)가 저장된 노드
- LinkedList : 부등호를 이용한 순차 검색 연산이 용이하도록 Leaf node 들을 LinkedList로 연결되어 있습니다.
SELECT 쿼리를 날리면 Root node에서 시작하여 Branch nodes를 거쳐 Leaf node 검색합니다.
각 노드에 저장된 key값을 순차적으로 비교하며, 현재 보고 있는 key가 찾으려는 key보다 작다면 왼쪽 Child Pointer를, 크다면 오른쪽 Child Pointer를 통해 자식 노드로 찾아갑니다.
참고자료
https://www.youtube.com/watch?v=liPSnc6Wzfk
'CS > Database' 카테고리의 다른 글
| MySQL Lock과 트랜잭션 격리 수준 정리 | 데이터베이스 Lock & Isolation Level 이해 (0) | 2025.03.16 |
|---|---|
| [Database] 데이터베이스 index, clustered index, non-clustered index 이해하기 (0) | 2024.09.18 |
| 데이터베이스 인덱스 종류와 원리: 희소 인덱스, 밀집 인덱스, 클러스터링 인덱스 (0) | 2024.02.28 |
| [DB] 데이터베이스의 원칙과 ACID, RDBMS와 NOSQL의 차이점 이해하기 (1) | 2023.10.09 |
| [DB] 데이터베이스 정규화란, 함수적 종속성, 이행적 종속성 - 제1정규화, 제2정규화, 제3정규화, BCNF (0) | 2022.10.09 |
인덱스란
- 데이터베이스 테이블의 검색 속도를 향상시키기 위한 자료구조로, 사전의 목차와 유사하다.
- 저장되는 컬럼의 값을 사용하여 항상 정렬된 상태를 유지합니다.
- 이러한 특징으로 인덱스는 쓰기 작업인 Insert, Update, Delete 연산 성능이 희생된다는 장점이 있습니다.
- 하지만 데이터베이스 작업은 읽기 작업이 80% 정도 일어나므로, 인덱스를 사용하는 것이 더 큰 장점이 있습니다.
InnoDB 스토리지 엔진에서는 Secondary Index(Primary Index를 제외한 모든 인덱스)의 리프 노드에는 레코드의 PK가 저장됩니다. 따라서 Secondary Index 검색에서는 레코드를 읽기 위해 PK를 가지고 있는 B-Tree를 다시 한번 검색해야 합니다. (1 + 1)
B Tree
자녀 노드의 최대 개수를 늘리기 위해서 부모 노드에 Key를 하나 이상 저장하는 자료구조.
이진 탐색 트리를 일반화한 트리라고도 합니다.
- Root Node: 최상위에 있는 노드
- Branch Node: 루트 노드와 리프 노드 중간에 있는 노드
- Leaf Node: 가장 하위에 있는 노드
- 리프 노드에는 실제 데이터 레코드를 찾아가기 위한 주소값을 가지고 있습니다.

- 부모 노드의 Key들을 오름차순으로 정렬합니다.
- 정렬된 순서에 따라 자녀 노드들의 key 값의 범위가 결정됩니다.
- ? < k1 / k1 < ? < k2 / ? > k2
B Tree 파라미터
- M : 각 노드의 최대 자녀 노드 수
- M이 3인 경우, 3차 B-Tree라고 부름
- M-1 : 각 노드의 최대 Key 수
- M을 정하면 자동으로 설정됨. M이 3인경우 각 노드의 Key는 최대 2개까지 가질 수 있음
- ⎡M/2⎤ : 각 노드의 최소 자녀 개수
- 3차 B-Tree에서는 최소 2개의 자녀 개수를 가집니다. (root node, leaf node 제외)
- ⎡M/2⎤ -1 : 각 노드의 최소 Key 수
- 3차 B-Tree에서는 최소 2개의 Key를 가집니다. (root node 제외)
잘못된 B-Tree 구조 보기

- Key가 2개인데, 자녀 노드의 개수가 2개이므로 잘못된 구조이다.
- Key가 3개이면 자녀 노드의 개수는 3개여야 함.

- Key가 1개인데, 자녀 노드의 개수가 3개이므로 잘못된 구조이다.
B-Tree
노드가 최소 하나의 Key는 가지기 때문에, N차 B-Tree인지와 상관없이 internal 노드는 최소 2개의 자녀 노드를 가집니다.
B Tree 데이터 삽입
- 추가는 항상 leaf 노드에 한다. (오름차순 순으로 추가한다.)
- 노드가 넘치면 가운데 Key를 기준으로 좌우 Key들은 분할하고, 가운데 Key는 승진한다.
- 노드가 넘친다 == 노드가 가질 수 있는 자녀의 개수 (M)
예시 1
1/2/15 key가 저장된 B Tree

2를 기준으로 왼쪽은 작은 값, 오른쪽은 큰 값이 저장된다.

- 위 상태에서 30이 추가되면 오른쪽 아래에 있는 노드에 추가되어 5, 15, 30 값을 가지게 됩니다.
- 3차 B Tree이므로 각 노드는 최대 2개의 Key를 가질 수 있으므로 변동이 필요합니다.
- 가운데 있는 15가 부모 노드로 승진합니다.
- 30은 15보다 크므로 3번째 자녀 노드에 위치시킵니다.

예시 2

현재 상황은 3번째 자녀 노드에 30, 90이 저장된 상태에서 20이 추가된 상황입니다.
- 20은 15보다 크므로 3번째 자녀 노드에 들어갑니다.
- 가운데에 있는 30은 부모 노드로 승진하고 90은 분리됩니다.
- 30이 부모 노드로 승진하면 부모 노드는 3개의 Key를 가지게 되어 변동이 필요합니다.
- 가운데에 있는 15 값을 부모 노드로 승진시킵니다.
- 승진 되면서 2와 30 값을 분리합니다.


예시 마지막 결과

B Tree 데이터 삭제

🔥 B Tree 계열을 Index로 사용하는 이유
먼저, 데이터베이스가 어디에 저장되고, 어떻게 조회하고 있는지 파악하기

Secondary Storage
- 데이터를 처리하는 속도가 가장 느리다.
- 데이터베이스는 보통 Secondary Storage에 해당함
- 데이터를 저장하는 용량이 가장 크다.
- Block 단위로 데이터를 읽고 쓴다.
- file system이 데이터를 읽고 쓰는 논리적인 단위
- block의 크기는 2의 승수로 표현된다.
- 불필요한 데이터까지 읽어올 가능성이 있다. (불필요한 데이터가 발생할 수 있음)
DB 관점 Secondary Storage
- DB에서 데이터를 조회할 때 최대한 적게 접근하는 것이 성능면에서 좋다.
- I/O 속도가 느리기 때문에
- block 단위로 읽고 쓰기 때문에, 연관된 데이터를 모아서 저장하면 더 효율적으로 읽고 쓸 수 있다.
- 추가로 조회된 데이터가 연관이 있는 경우, 추가 조회 없이 데이터를 조회할 수 있다.
AVL Tree vs B Tree
AVL Tree도 B Tree와 마찬가지로 모든 연산에 대해 O(log n)의 시간 복잡도를 가지고 있는데, B Tree를 인덱스 자료구조로 사용하는 이유
1. AVL Tree

Root Node만 메모리에 올라가 있다고 하면
where b = 5를 탐색할 때
- 3번 노드 (1번 조회)
- 4번 노드 (1번 조회)
- 5번 노드 (1번 조회)
- 5번 노드의 포인터 값 조회 (1번 조회)
- 총 4번의 조회가 발생합니다.
2. B-Tree

Root Node만 메모리에 올라가 있다고 하면
where b = 5를 탐색할 때
- 가운데 리프 노드 (1번 조회)
- 가운데 리프 노드 5번 Key에 포인터 값 조회 (1번 조회)
- 총 2번의 조회 발생합니다.
AVL Tree vs B Tree 결론

B-Tree는 AVL 트리와 달리, 자녀 노드의 개수를 설정할 수 있어, Secondary Storage와의 조회 요청을 단축시킬 수 있습니다.
데이터를 찾을 때 탐색 범위를 빠르게 좁힐 수 있어, Index 자료구조로 사용된다.
추가 예시) 101차 B-Tree
M = 101 / 하나의 노드는 101개의 자녀 노드를 가질 수 있으며, 100개의 key를 가질 수 있음

- 높이 3으로 약 1억개의 데이터를 저장할 수 있음
101차 B-Tree Worst Case

- 4개의 레벨, 높이 3만으로도 수 백만, 수 천만 개의 데이터를 저장할 수 있다.
B Tree 정리
- 자녀 노드의 최대 개수를 늘리기 위해서 부모 노드에 Key를 하나 이상 저장하는 자료구조이다.
- B-Tree는 AVL 트리와 달리, 자녀 노드의 개수를 설정할 수 있어, Secondary Storage와의 조회 요청을 단축시킬 수 있다.
- 노드가 최소 하나의 Key는 가지기 때문에, N차 B-Tree인지와 상관없이 internal 노드는 최소 2개의 자녀 노드를 가진다.
- 101차 B Tree 구조를 통해 26,5301 < avg size < 1,0406,0400 개의 데이터를 4개의 level과 3번의 move로 처리할 수 있다.
B+Tree
B Tree와 차별화된 특징으로는
- B+Tree의 리프 노드는 서로 연결 리스트로 연결되어 있습니다. 형제 노드끼리 옮겨가며 조회가 가능합니다.
- internal 노드에는 Key만 저장되며, 이 Key를 사용해서 자식 노드의 저장공간 상 위치를 판단합니다.
- 데이터를 찾기 위한 포인터도 리프 노드에만 있습니다.
- internal 노드의 데이터 크기를 줄여 메모리 사용이 효율적입니다.

- Root node : 최상단 노드, 검색 경로의 출발점
- Branch node : Leaf node까지 가기 위해 다음 경로 노드의 key 값(데이터를 위한 인덱스)을 가지고 있는 노드
- Leaf node : 인덱스(key)와 함께 실제 검색할 데이터(value)가 저장된 노드
- LinkedList : 부등호를 이용한 순차 검색 연산이 용이하도록 Leaf node 들을 LinkedList로 연결되어 있습니다.
SELECT 쿼리를 날리면 Root node에서 시작하여 Branch nodes를 거쳐 Leaf node 검색합니다.
각 노드에 저장된 key값을 순차적으로 비교하며, 현재 보고 있는 key가 찾으려는 key보다 작다면 왼쪽 Child Pointer를, 크다면 오른쪽 Child Pointer를 통해 자식 노드로 찾아갑니다.
참고자료
https://www.youtube.com/watch?v=liPSnc6Wzfk
'CS > Database' 카테고리의 다른 글
| MySQL Lock과 트랜잭션 격리 수준 정리 | 데이터베이스 Lock & Isolation Level 이해 (0) | 2025.03.16 |
|---|---|
| [Database] 데이터베이스 index, clustered index, non-clustered index 이해하기 (0) | 2024.09.18 |
| 데이터베이스 인덱스 종류와 원리: 희소 인덱스, 밀집 인덱스, 클러스터링 인덱스 (0) | 2024.02.28 |
| [DB] 데이터베이스의 원칙과 ACID, RDBMS와 NOSQL의 차이점 이해하기 (1) | 2023.10.09 |
| [DB] 데이터베이스 정규화란, 함수적 종속성, 이행적 종속성 - 제1정규화, 제2정규화, 제3정규화, BCNF (0) | 2022.10.09 |
