파이썬 머신러닝 가이드 책을 참고하였습니다.
목차
1. 회귀란
2. 경사 하강법
3. 평가 지표 (MSE, MAE, RMSE)
4. 다항 회귀
(1) 회귀
머신러닝의 (선형) 회귀는
실제 값과 예측값의 차이를 최소화하는 식을 찾는 것으로, 즉) y=wx+b의 식에서 독립변수의 값에 영향을 미치는 회귀 계수(Regression Coefficients)의 최적의 값을 찾는 것입니다.
( y = 종속 변수, w, b = 독립 변수의 값에 영향을 미치는 회귀 계수, x = 독립 변수 )
예를 들어, 주택 가격이 주택의 크기로만 결정된다고 하면, 종속 변수 = 주택 가격 / 독립 변수 = 주택 크기라고 할 수 있습니다.
여러 개의 독립 변수와 한 개의 종속변수 간의 상관 관계를 모델링하는 기법이다.
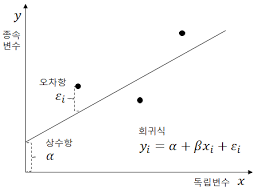
실제 값과 회귀 모델의 차이에 따른 오류 값을 남은 오류, 즉 잔차라고 한다.
최적의 회귀 모델은 전체 데이터의 잔차(오류 값) 합이 최소가 되는 모델을 만드는 것이다.
오류 값은 +(양수)나 -(음수)가 될 수 있습니다.
그래서 보통 오류 합을 계산할 때는 절댓값을 취해서 더하거나 MAE (Mean Absolute Error), 오류 값의 제곱을 구해서 더하는 방식 RSS (Residual Sum of Square)을 취합니다.
회귀에서 이 RSS는 비용이며 w 변수(회귀계수)로 구성되는 RSS를 비용 함수 또는 손실 함수라고 합니다.
(2) 경사 하강법 ( 비용 최소화 하기)
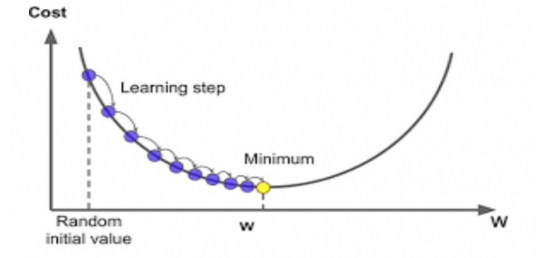
사전적 의미로 '점진적인 하강'이라는 뜻으로, 점진적으로 반복적인 계산을 통해 W 파라미터 값을 업데이트하면서 오류 값이 최소가 되는 W 파라미터를 구하는 방식을 의미합니다.
경사하강법은 반복적으로 비용 함수의 반환 값, 즉 예측값과 실제 값의 차이가 작아지는 방향성을 가지고 W 파라미터를 지속해서 보정해 나갑니다.
(3) 회귀 평가 지표
: 실제 값과 예측값의 차이를 기반으로 한다.
| MAE | 실제 값과 예측값의 차이를 절댓값으로 변환해 평균한 것이다. |
| MSE | 실제 값과 예측값의 차이를 제곱해 평균한 것이다. |
| RMSE | MSE에 루트를 씌운 것이다. (MSE 값은 오류의 제곱을 구하므로 실제 오류 평균보다 더 커지는 특성이 있어 RMSE 값을 이용하기도 한다.) |
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error
print('MAE : ', mean_absolute_error(y_tert,y_pred))
print('MSE : ', mean_squared_error(y_test, y_pred))
print('RMSE : ', np.sqrt(mean_squared_error(y_test, y_pred))
[모델 성능지표& Python 코드] Regression - 성능 측정 지표 총정리
머신러닝은 데이터 가공/변환 , 모델 학습/ 예측 그리고 평가의 프로세스로 구성된다. 즉 머신러닝 및 딥러닝 그리고 데이터 모델에대한 최종적인 평가는 성능지표를 통하여 판단하게 된다. 이
hofe-rnd.tistory.com
공부하는데 참고하였으며, 다양한 평가지표가 설명되어 있어 공유합니다!
EX) 사이킷런 LinearRegression 클래스
예측값과 실제 값의 RSS를 최소화해 OLS(Ordinary Least Squares) 추정 방식으로 구현한 클래스이다.
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
lr = LinearRegression()
lr.fit(x_train, y_train)
pred = lr.predict(x_test)
mse = mean_squared_error(y_test, pred)
rmse = np.sqrt(mse)
print('절편 값 :', lr.intercept_)
print('회귀 계수 값 :', np.round(lr.coef_, 1))파라미터
* fit_intercept : intercept (절편) 값을 계산할 것인지 말지를 지정한다. (default = True)
속성
* coef_ : 회귀 계수가 배열 형태로 저장한다. Shape는 (Target 값 개수, 피처 개수)
* intercept_ : intercept(절편) 값
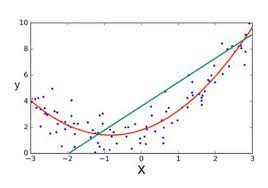
(4) 다항 회귀 (y=β0+β1x+β2x2+⋯+βmxm+ϵ)
회귀가 독립 변수의 단항식이 아닌 2차, 3차 방정식과 같은 다항식으로 표현되는 것을 다항 회귀(Polynomial)라고 한다.
EX) 사이킷런 PolynomialFeatures
위 클래스를 통해 피처를 다항식 피처로 변환하여 회귀 모델에 적용하여 다항 회귀를 구현한다.
PolynomialFeatures 클래스는 degree 파라미터를 통해 입력받은 단항식 피처를 degree에 해당하는 다항식 피처(차수)로 변환한다.
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
poly = PolynomialFeatures(degree=3)
poly.fit(x_train)
poly_ftr = poly.transform(x_train)
lr_model = LinearRegression()
lr_model.fit(poly_ftr, y_train)
pred = lr_model.predcit(x_test)
[ML] 머신러닝 결정트리 (DecisionTreeClassifier, DecisionTreeRegressor)
[ML] 머신러닝 결정트리 (DecisionTreeClassifier, DecisionTreeRegressor)
파이썬 머신러닝 완벽 가이드 책을 참고하였습니다. (1) DecisionTreeClassifier, DecisionTreeRegressor 결정 트리 데이터에 있는 규칙을 학습을 통해 자동으로 찾아내 트리 기반의 분류 규칙을 만든다. 일반
kylo8.tistory.com
'AI > Machine Learning' 카테고리의 다른 글
| [머신러닝] 비지도학습 K-평균 알고리즘 및 실루엣 계수 (0) | 2023.02.16 |
|---|---|
| [Numpy] - expand_dims 차원 추가하기 (0) | 2022.06.16 |
| 머신러닝 스태킹 앙상블 기법 이해와 Python 구현 사례 (0) | 2022.04.09 |
| 불균형 데이터 처리를 위한 언더 샘플링과 오버 샘플링 (0) | 2022.04.09 |
| [ML] 머신러닝 - 부스팅 GBM, XGBoost, LightGBM (0) | 2022.04.09 |
파이썬 머신러닝 가이드 책을 참고하였습니다.
목차
1. 회귀란
2. 경사 하강법
3. 평가 지표 (MSE, MAE, RMSE)
4. 다항 회귀
(1) 회귀
머신러닝의 (선형) 회귀는
실제 값과 예측값의 차이를 최소화하는 식을 찾는 것으로, 즉) y=wx+b의 식에서 독립변수의 값에 영향을 미치는 회귀 계수(Regression Coefficients)의 최적의 값을 찾는 것입니다.
( y = 종속 변수, w, b = 독립 변수의 값에 영향을 미치는 회귀 계수, x = 독립 변수 )
예를 들어, 주택 가격이 주택의 크기로만 결정된다고 하면, 종속 변수 = 주택 가격 / 독립 변수 = 주택 크기라고 할 수 있습니다.
여러 개의 독립 변수와 한 개의 종속변수 간의 상관 관계를 모델링하는 기법이다.

실제 값과 회귀 모델의 차이에 따른 오류 값을 남은 오류, 즉 잔차라고 한다.
최적의 회귀 모델은 전체 데이터의 잔차(오류 값) 합이 최소가 되는 모델을 만드는 것이다.
오류 값은 +(양수)나 -(음수)가 될 수 있습니다.
그래서 보통 오류 합을 계산할 때는 절댓값을 취해서 더하거나 MAE (Mean Absolute Error), 오류 값의 제곱을 구해서 더하는 방식 RSS (Residual Sum of Square)을 취합니다.
회귀에서 이 RSS는 비용이며 w 변수(회귀계수)로 구성되는 RSS를 비용 함수 또는 손실 함수라고 합니다.
(2) 경사 하강법 ( 비용 최소화 하기)
사전적 의미로 '점진적인 하강'이라는 뜻으로, 점진적으로 반복적인 계산을 통해 W 파라미터 값을 업데이트하면서 오류 값이 최소가 되는 W 파라미터를 구하는 방식을 의미합니다.
경사하강법은 반복적으로 비용 함수의 반환 값, 즉 예측값과 실제 값의 차이가 작아지는 방향성을 가지고 W 파라미터를 지속해서 보정해 나갑니다.

(3) 회귀 평가 지표
: 실제 값과 예측값의 차이를 기반으로 한다.
| MAE | 실제 값과 예측값의 차이를 절댓값으로 변환해 평균한 것이다. |
| MSE | 실제 값과 예측값의 차이를 제곱해 평균한 것이다. |
| RMSE | MSE에 루트를 씌운 것이다. (MSE 값은 오류의 제곱을 구하므로 실제 오류 평균보다 더 커지는 특성이 있어 RMSE 값을 이용하기도 한다.) |
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error
print('MAE : ', mean_absolute_error(y_tert,y_pred))
print('MSE : ', mean_squared_error(y_test, y_pred))
print('RMSE : ', np.sqrt(mean_squared_error(y_test, y_pred))
[모델 성능지표& Python 코드] Regression - 성능 측정 지표 총정리
머신러닝은 데이터 가공/변환 , 모델 학습/ 예측 그리고 평가의 프로세스로 구성된다. 즉 머신러닝 및 딥러닝 그리고 데이터 모델에대한 최종적인 평가는 성능지표를 통하여 판단하게 된다. 이
hofe-rnd.tistory.com
공부하는데 참고하였으며, 다양한 평가지표가 설명되어 있어 공유합니다!
EX) 사이킷런 LinearRegression 클래스
예측값과 실제 값의 RSS를 최소화해 OLS(Ordinary Least Squares) 추정 방식으로 구현한 클래스이다.
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
lr = LinearRegression()
lr.fit(x_train, y_train)
pred = lr.predict(x_test)
mse = mean_squared_error(y_test, pred)
rmse = np.sqrt(mse)
print('절편 값 :', lr.intercept_)
print('회귀 계수 값 :', np.round(lr.coef_, 1))파라미터
* fit_intercept : intercept (절편) 값을 계산할 것인지 말지를 지정한다. (default = True)
속성
* coef_ : 회귀 계수가 배열 형태로 저장한다. Shape는 (Target 값 개수, 피처 개수)
* intercept_ : intercept(절편) 값
(4) 다항 회귀 (y=β0+β1x+β2x2+⋯+βmxm+ϵ)
회귀가 독립 변수의 단항식이 아닌 2차, 3차 방정식과 같은 다항식으로 표현되는 것을 다항 회귀(Polynomial)라고 한다.

EX) 사이킷런 PolynomialFeatures
위 클래스를 통해 피처를 다항식 피처로 변환하여 회귀 모델에 적용하여 다항 회귀를 구현한다.
PolynomialFeatures 클래스는 degree 파라미터를 통해 입력받은 단항식 피처를 degree에 해당하는 다항식 피처(차수)로 변환한다.
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
poly = PolynomialFeatures(degree=3)
poly.fit(x_train)
poly_ftr = poly.transform(x_train)
lr_model = LinearRegression()
lr_model.fit(poly_ftr, y_train)
pred = lr_model.predcit(x_test)
[ML] 머신러닝 결정트리 (DecisionTreeClassifier, DecisionTreeRegressor)
[ML] 머신러닝 결정트리 (DecisionTreeClassifier, DecisionTreeRegressor)
파이썬 머신러닝 완벽 가이드 책을 참고하였습니다. (1) DecisionTreeClassifier, DecisionTreeRegressor 결정 트리 데이터에 있는 규칙을 학습을 통해 자동으로 찾아내 트리 기반의 분류 규칙을 만든다. 일반
kylo8.tistory.com
'AI > Machine Learning' 카테고리의 다른 글
| [머신러닝] 비지도학습 K-평균 알고리즘 및 실루엣 계수 (0) | 2023.02.16 |
|---|---|
| [Numpy] - expand_dims 차원 추가하기 (0) | 2022.06.16 |
| 머신러닝 스태킹 앙상블 기법 이해와 Python 구현 사례 (0) | 2022.04.09 |
| 불균형 데이터 처리를 위한 언더 샘플링과 오버 샘플링 (0) | 2022.04.09 |
| [ML] 머신러닝 - 부스팅 GBM, XGBoost, LightGBM (0) | 2022.04.09 |
